Wikipediaの電車のページを読んでいると「かご形三相誘導電動機」という単語が頻繁に登場する.
電車を動かすためのモータとして,この電動機が使われている.
誘導電動機(モータ)については,学部3年の講義(電力機器工学)で勉強した.
しかし,講義では基礎の理論が中心だった.
実際に電車を動かしている誘導機(かご形三相誘導電動機)について知りたい,と思って勉強してみた.
- かご形って何?どういう構造?
- 固定子と回転子?
- なんで「すべり」が発生するのか?
上記3点を中心にしながら,基本原理についてまとめてみる.
三相誘導電動機(モータ)の回転原理
電動機は,電気エネルギー(電力)を運動エネルギー(回転)に変換する.
(発電機は,運動エネルギーを電気エネルギーに変換する)
その中でも(三相)誘導電動機は,「交流」の電力を用いて運動エネルギーを生み出す.
交流の電力を用いる電動機は,ほかに同期電動機がある.
いずれも,電動機中の回転磁界を制御することによって,スピードを制御する.
誘導機回転にかかわる物理法則
ファラデーの法則(e=-dφ/dt)
磁束の増減に対し,それを補う方向に起電力 \( e \)を生じる.
$$ e=-\frac{d\phi}{dt} $$
起電力が生じると,電圧が高い方から低い方へ電流が流れる.
小学校の理科の実験で,コイル中へ棒磁石を出し入れすると,コイルへ電流が流れる(電流計の針が振れる)というあの物理現象だ.
フレミングの左手の法則(F=I×B)
磁束 \(\boldsymbol{B}\) 中における導体に
電流 \(\boldsymbol{I}\) を流すと,
電磁力 \( \boldsymbol{F} \) が生じる.
電磁力の方向は, \( \boldsymbol{I} \times \boldsymbol{B} \)の方向.
$$ \boldsymbol{F}=\boldsymbol{I} \times \boldsymbol{B} $$
これは「フレミング左手の法則」とも呼ばれる.
誘導機においては,電流 \( \boldsymbol{I} \)がファラデーの法則にしたがって誘導される.
これが磁束中に流れることで,電磁力(すなわち機械力)が生じる.
「アラゴの円板」
誘導機の動作原理として「アラゴの円板」という装置が知られている.
この装置は,先に挙げた
- ファラデーの法則
- フレミングの左手の法則
に従って動作する.
円板は良導体(電気をよく通す),その円板を挟むようにU字磁石を設置してある.
磁石はN極とS極をもっており,N⇒Sの向きに磁界が生じている.
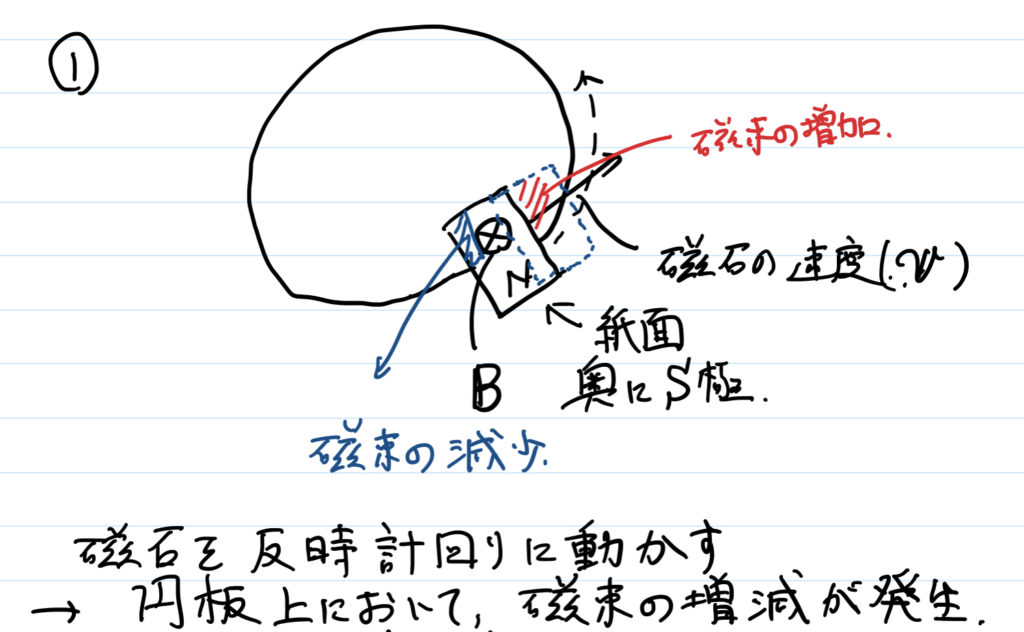
この装置において,まず磁石を円周方向(この図では反時計回り)に沿って動かす.すると,円板上において磁束の増減が発生する.(\( \frac{dB}{dt}\neq 0 \))
(進行方向では,紙面奥向きの磁束が増えようとする.)
(磁石が離れていく側では,紙面奥向きの磁束が減ろうとする.)
導体において磁束の増減が存在すると,ファラデーの法則にしたがって起電力が発生する.すなわち,
- 進行方向側で磁束を減少させ,
- 進行方向逆側で磁束を増加させる
方向の起電力が生じる.
良導体である円板上に起電力が発生すると,電流(誘導電流)が流れる.
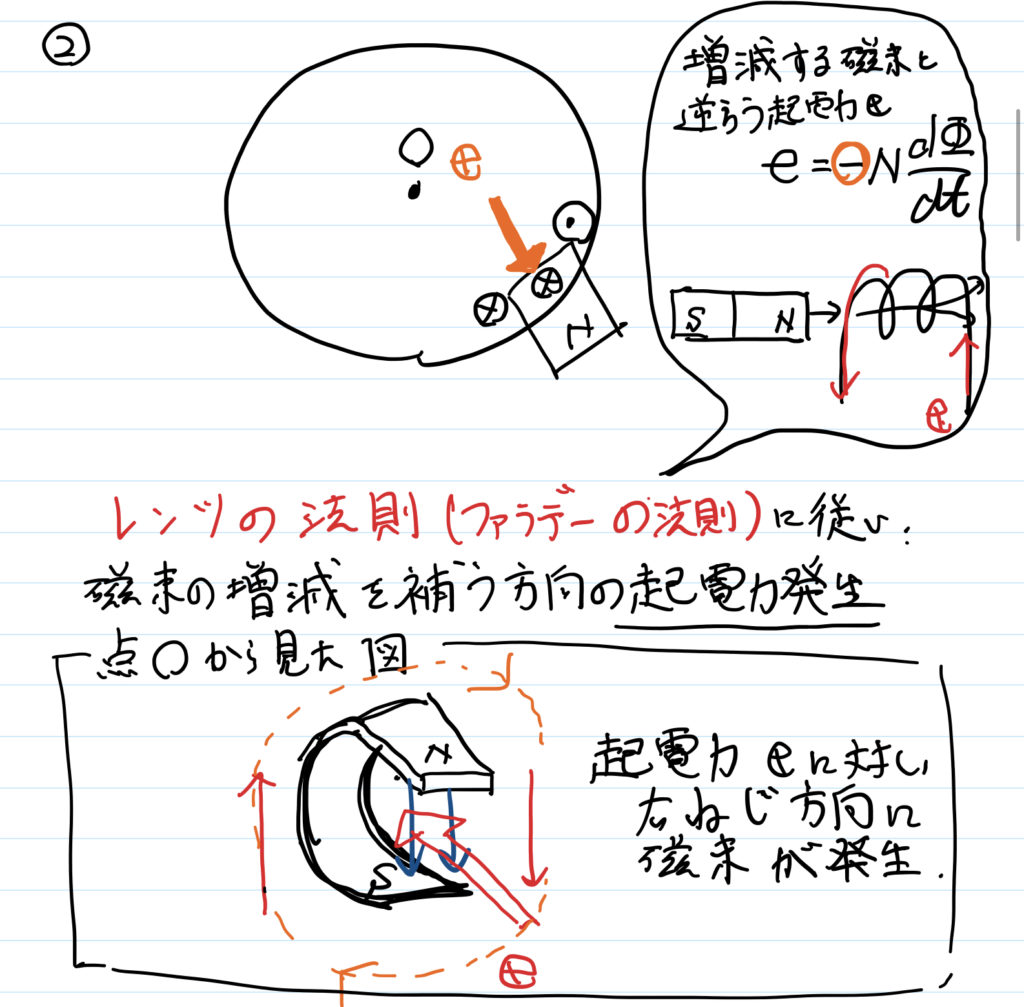
電流の周囲には右ネジ方向の磁界が発生する.
そのため,磁石進行方向で紙面奥向きの磁束を打ち消す起電力を生じる.
それはすなわち,起電力が円板の半径方向外向きに生じるということだ.
生じた起電力によって,円板上には渦電流が生じる.
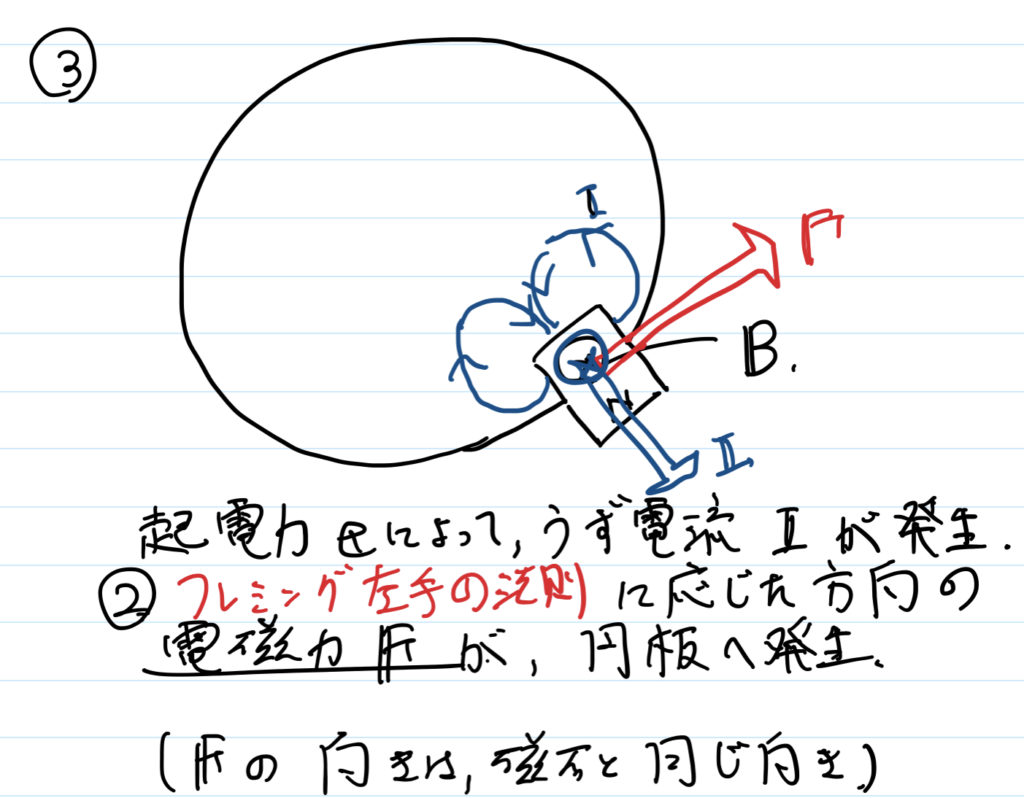
起電力の有無にかかわらず,円板上には紙面奥向きの磁界(磁束 \( \boldsymbol{B} \))が生じている.また,磁石に向かうような誘導電流 \( \boldsymbol{I} \) が流れている.
ゆえに,フレミング左手の法則に応じた方向の電磁力 \( \boldsymbol{F} \) が,円板導体に発生する.
電磁力の方向は,電流 \( \boldsymbol{I} \) と磁束 \( \boldsymbol{B} \) の外積方向である.
したがって,導体へ加わる電磁力の方向は,磁石と同じ反時計回りの方向となる.
この電磁力が,誘導機を動かす回転力となる.
「すべり」の発生
この装置における円板の速度は,磁石の速度(ここでは \( \boldsymbol{v} \) とする)よりも小さくなる.
もし,円板の速度=磁石の速度となると・・・
- 磁石-円板間の相対速度が0
- 円板導体上での磁束の増減がなくなる
- 誘導起電力が発生しなくなる
- 電磁力が生じなくなる
このようになって,電磁力が生じなくなり,導体を回転させられない.
円板が磁石に誘導されて回転するためには,必ず磁石からの遅れが必要なのだ.
誘導機では,この遅れ(導体の磁石に対する遅れ)を「すべり」と呼ぶ.
かご形の回転子・固定子(界磁)
ここまでは,アラゴの円板を用いて誘導機の動作原理を説明してきた.
誘導機においても,「磁石」と「円板導体」に対応するものがある.それぞれ,
- 電流を誘導する磁石=固定子
- 電磁力によって回転する円板=回転子
と呼ばれる.
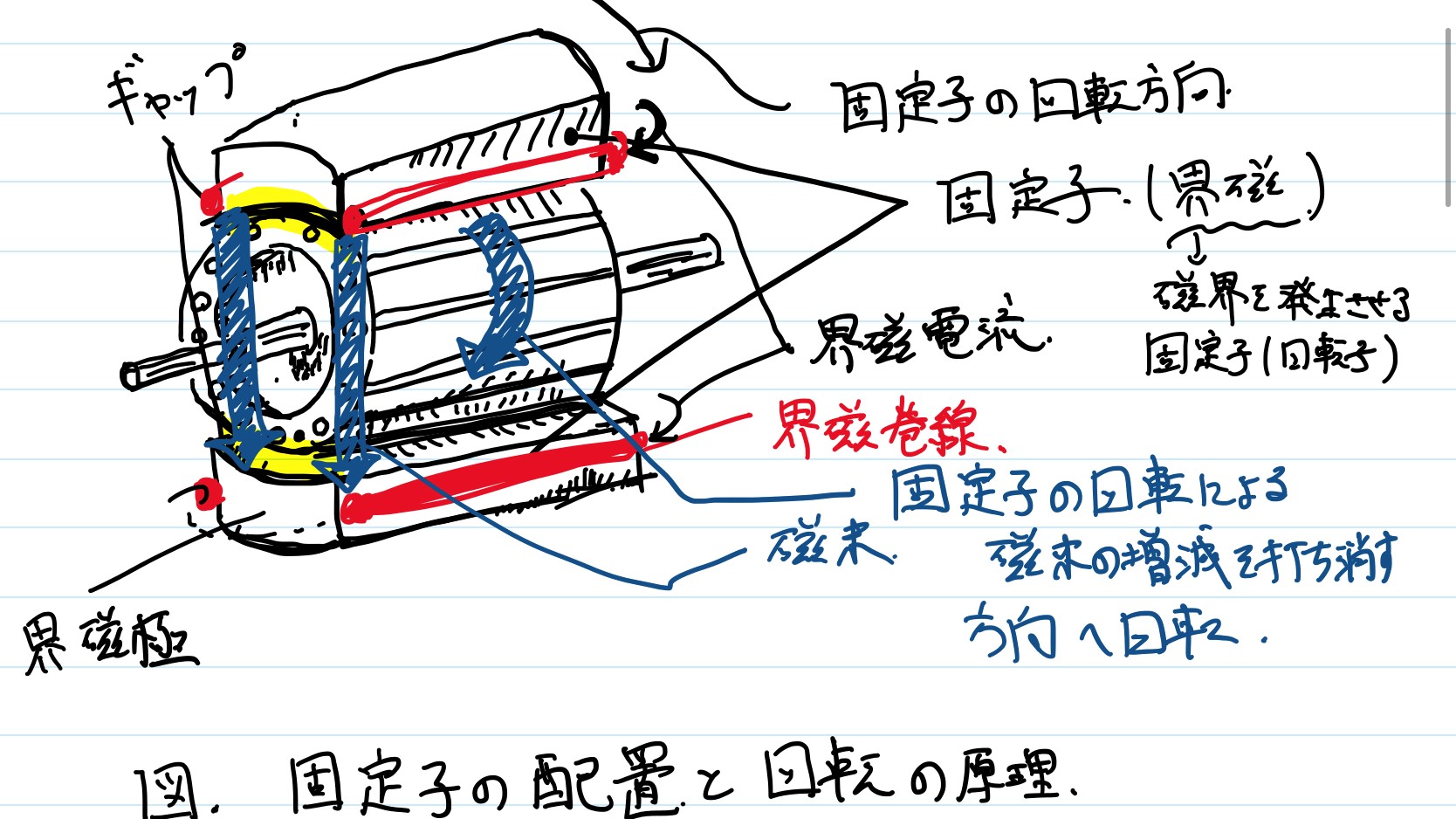
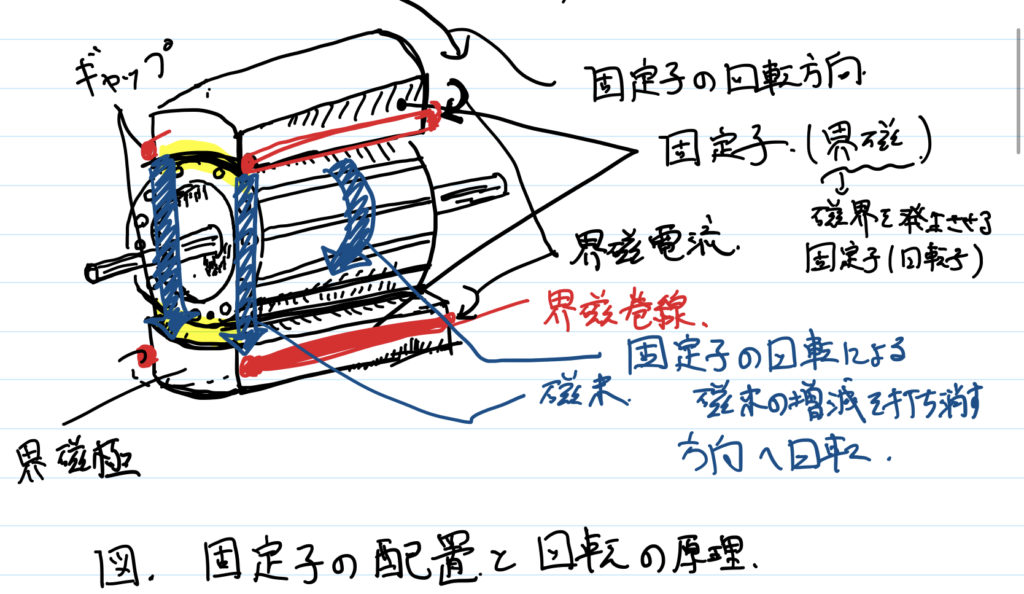
「かご形」誘導電動機では,回転子と固定子は以下の図のように配置されている.

この図において,「アラゴの円板」の動作原理をそのまま当てはめる.
固定子は「界磁」と呼ばれる.界磁極が,磁界を発生させる.
界磁が回転することで,磁束の増減が発生する.
この磁束の増減を打ち消すように,回転子の導体棒に電流が生じる.
界磁極間の磁束と,導体棒の電流によって,回転子に電磁力が生じる.
このような流れで,回転子が回転するのだ.回転子は次の図のような構造をもつ.
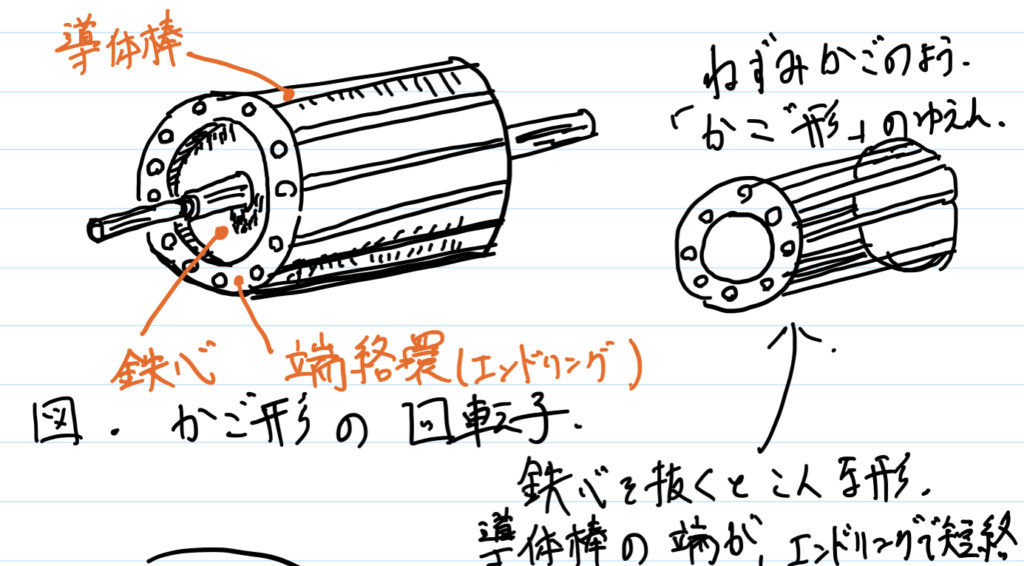
中央には,良導体である鉄心が設置されている.
また,鉄心まわりの導体棒は,ねずみかごのように配置されている.
これが「かご形」誘導機と呼ばれるゆえん.
導体の端は,エンドリングで短絡されている.
以上が,誘導電動機が回転する原理.
ただ,固定子(磁石)を機械的に運動させるわけにはいかない.
(回転力を生み出すために,固定子を回転させる運動エネルギーを必要とするのは本末転倒である・・・)
そこで実際の誘導機では,固定子の回転を電気的に行っている.
これにより,磁束を回転させ,電磁力を発生している.
三相交流による磁界の電気的回転
電気的な回転は,「交流」の電力によって行われる.
「交流」は,コンセントにやってきている電力と同じ形式.
実効値0であり,周期的に正負が入れ替わる電力のこと.
かご形三相誘導電動機では,磁界の回転に「三相交流」を用いる.
固定子は,1相あたり複数の界磁極・巻線が設置されている.
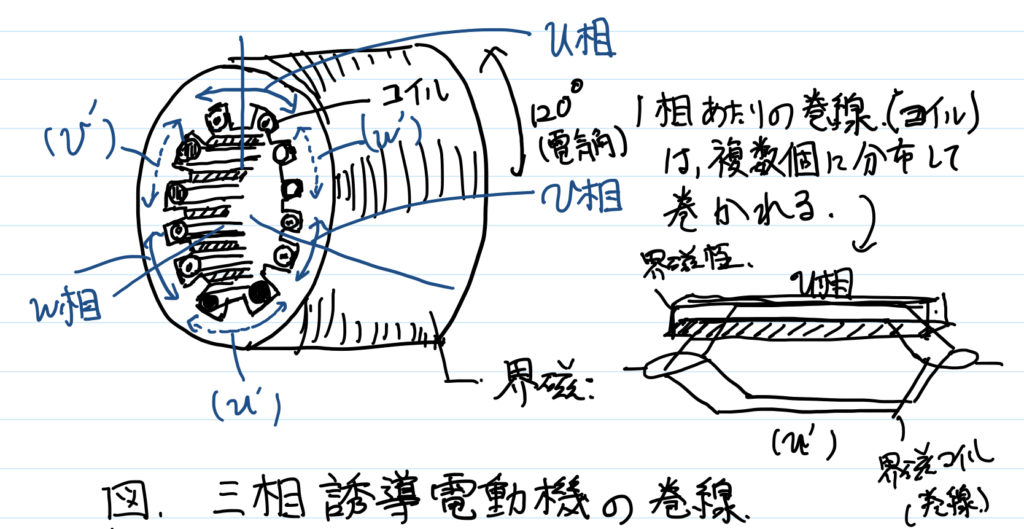
固定子1周に,三相(u相,v相,w相)を均等に配置していることになる.
この各相へ三相電流を流すことで,界磁極間には磁束が生じる.
これらの合成磁束による起磁力が,交流電流の変化によってグルグルと回転する.
合成磁束が1回転する周期は,1相の電流サイクルに等しい.
ことばではわかりづらいので,図で説明していく.
まず,各相には,120°ずつずれた交流電流を流す(下図)
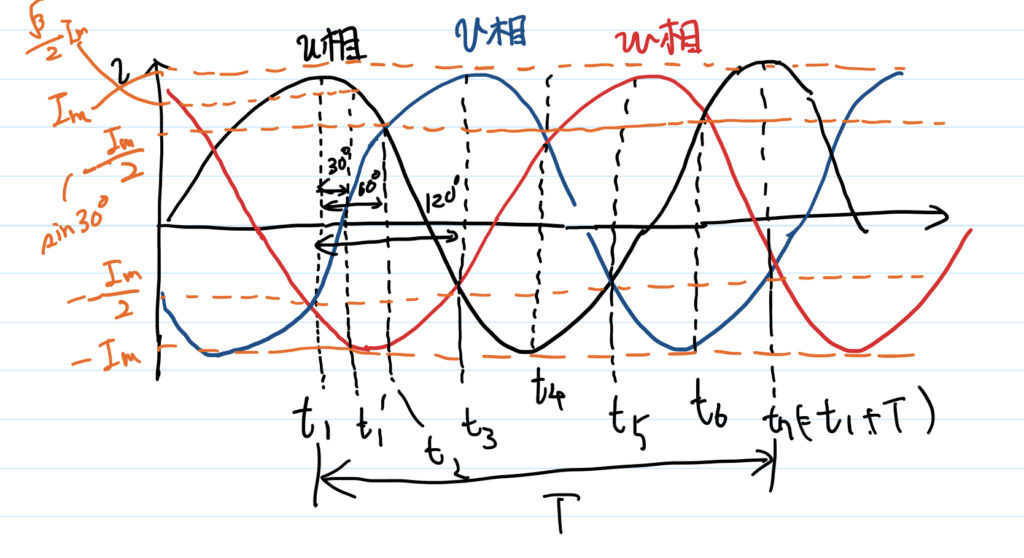
次の図以降で,同図中に示した各時刻における,電流と磁束の分布を示す.
時刻 \( t_1 \) においては,u相が波高値( \( I_\mathrm{m} \) ),v相,w相が波高値の1/2の電流値となっている(上図電流波形を参照).
したがって,鉄心へ生じる磁束は下図左の赤線のようになる.
これらを合わせた合成磁束は,同図中黄色い矢印となる.
時刻 \( t_1^{\prime} \) は,\( t_1 \) から30°(1/12周期)進んだ時刻である.
同時刻において,各相の電流値は,u相が波高値の \( \sqrt{3}/2 \) 倍,v相が0,w相が波高値の \( -\sqrt{3}/2 \) 倍となっている.
したがって,鉄心へ生じる磁束は下図右の赤線のようになる.
これらを合わせた合成磁束は,同図中黄色い矢印となる.
時刻 \( t_1 \) の合成磁束から,30°時計方向へ回った磁束となる.
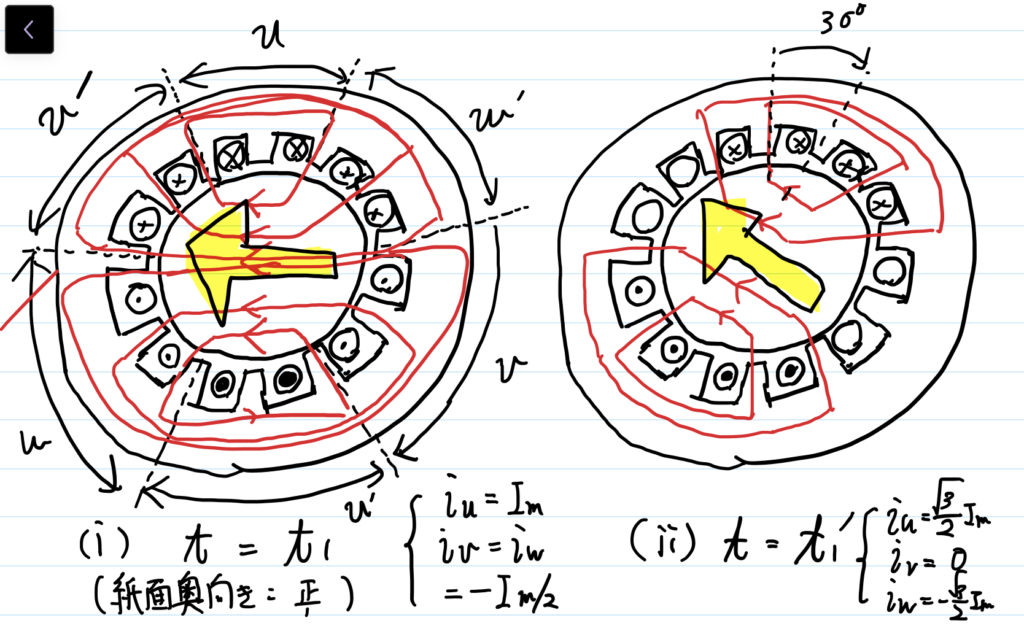
時刻 \( t_2 \) は,\( t_1 \) から60°(1/6周期)進んだ時刻である.
同時刻において,各相の電流値は,u相・v相が波高値の \( 1/2 \) 倍,w相が波高値の \( -1 \) 倍となっている.
したがって,鉄心へ生じる磁束は下図左の赤線のようになる.
これらを合わせた合成磁束は,同図中黄色い矢印となる.
時刻 \( t_2 \) の合成磁束から,60°時計方向へ回った磁束となる.
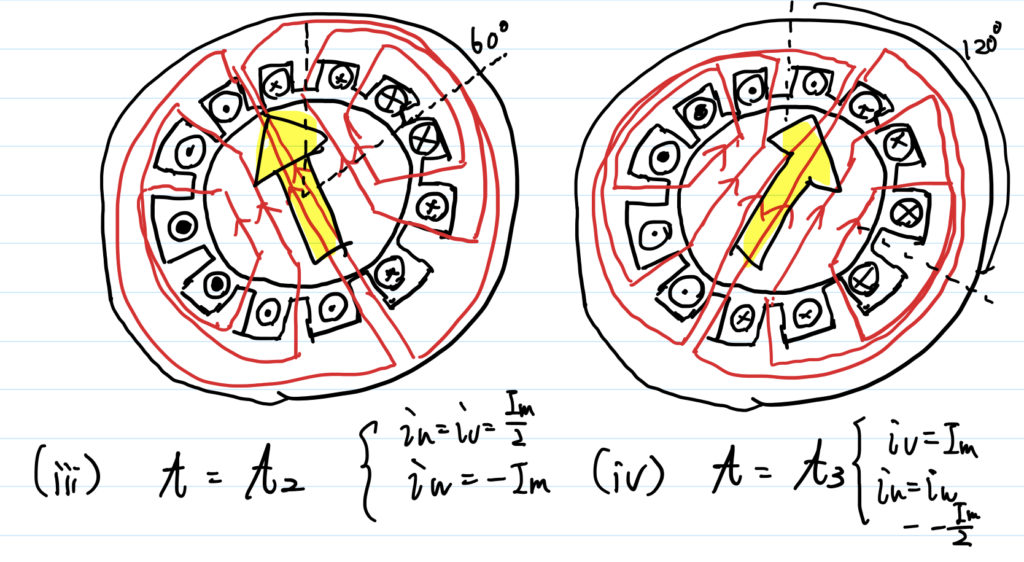
このような形で,時間の経過によって,合成磁束が回転していく.
\( t_3 \) 以降における合成磁束も,自分で作図していくと理解できる.
ここでは,図(iv)~(vii)に,\( t_3 \) 以降の合成磁束を示している.
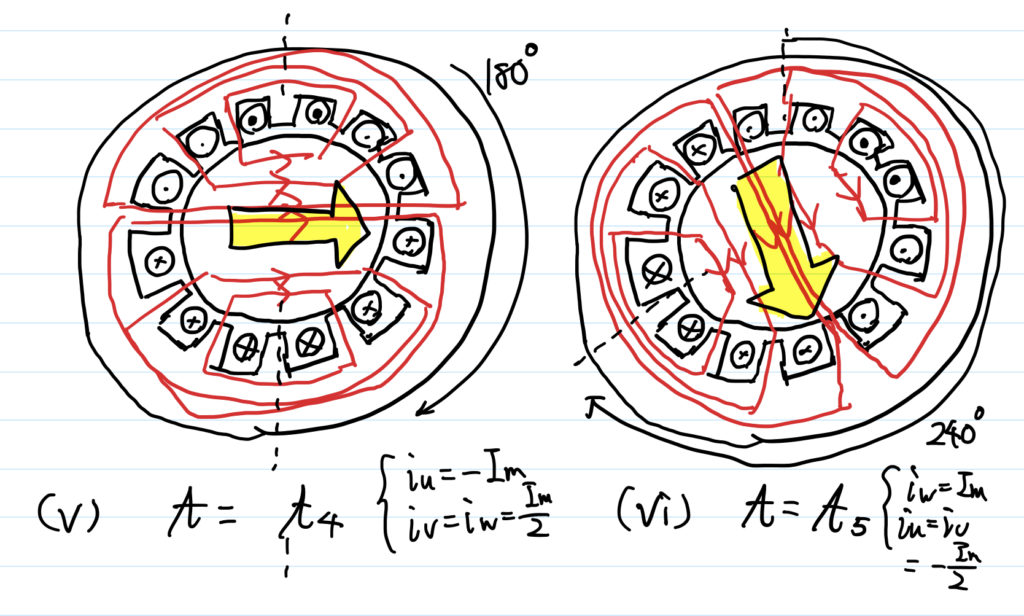
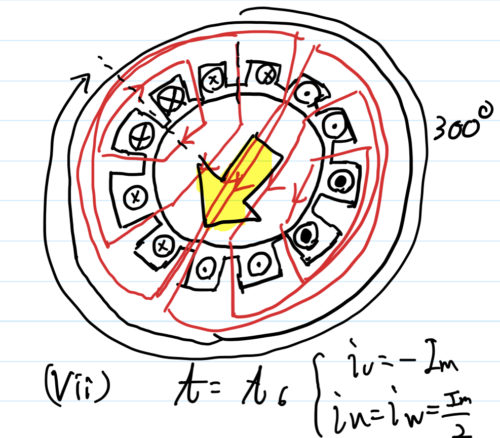
このようにして,固定子を電気的に回転させることで,回転子における合成磁束を回している.
回転する磁束中で,導体へ渦電流が生じ,
それらがフレミングの左手の法則にしたがって,電磁力が発生する.
これによって回転子が回るのだ.
まとめ:電車の主電動機

以上,かご形三相誘導電動機の回転原理についてまとめてみた.
自分が勉強したことをそのまままとめただけなので,
わかりづらかったかもしれない.
Wikipediaでよく見るあれって,どうやって動いてるのかな~という疑問を解消できた.
モータの制御方法についても,別記事でまとめてみようと思う.
参考文献
坪島茂彦:「図解 誘導電動機 -基礎から制御まで-」,東京電機大学出版局 (2003)
関連記事